最小生成树

发表于2021-09-20更新于2021-10-13阅读次数

kruskal prim ..

kruskal

  • 思路 贪心，每次选择权值最小的边，保证每次加入新边不会生成环
  • 难点 如何判定生成环，方法：保证新加入的边的两个端点，不都在已加入的边的端点集合中，用并查集实现
  • 链式前向星模板 时间O(m*logm)(m为边数)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
//链式前向星(kruskal用邻接矩阵不太好写)-----------------------------------
/*** 
 * @Practice Win
 * 洛谷 P3366 【模板】最小生成树
 * 最小生成树 板子题
 */
#include<bits/stdc++.h>
#pragma comment(linker, "/STACK:102400000,102400000")//解决递归函数多次调用栈溢出问题
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
typedef long long ll;
#define INF 0x7fffffff//10^9级别，不到2^32
const ll maxn=1e4+11;//最多点数！！！
const ll maxm=1e6+11;//最多边数！！！
struct Edge{
	ll fr,to,w,next;
}edge[maxm];//边集，下标从1开始！！！
ll fa[maxn],head[maxn];
ll n,m,tmp;
void add(ll u,ll v,ll w){
	edge[tmp].fr=u; edge[tmp].to=v; edge[tmp].w=w;
	edge[tmp].next=head[u];
	head[u]=tmp++;
}
bool cmp(Edge a,Edge b){
	return a.w<b.w;
}
ll found(ll x){
	return fa[x]==x?x:fa[x]=found(fa[x]);
}
ll kruskal(){//若存在最小生成树，返回其最小权值和,并输出，若不存在，返回一个错误值，并输出“orz”
	sort(edge+1,edge+tmp,cmp);
	ll cnt=0,ans=0;
	for(ll i=1;i<tmp;i++){//边编号从1开始！！！
		ll fu=found(edge[i].fr);//并查集得到fu和fv
		ll fv=found(edge[i].to);
		if(fu==fv) continue;//若在同一集合，则跳过，说明这两个点都已被使用过
		fa[fu]=fv;//合并
		cnt++;
		ans+=edge[i].w;
		if(cnt==n-1)  break;
	}
	if(cnt==n-1)  cout<<ans<<endl;
	else  cout<<"orz"<<endl;
	return ans;
}
void makset(){
	for(ll i=1;i<=n;i++)  fa[i]=i;//点的编号应与题目相符合！！！
}
void init(){
	memset(head,-1,sizeof(head));
	tmp=1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
	cin>>n>>m;
    init();
    makset();
    for(ll i=1;i<=m;i++){
        ll u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);//有向图
		//add(v,u,w);//无向图
    }
    kruskal();
    return 0;
}

灵活运用，唯一最小生成树（思维）

题目链接 https://vjudge.net/problem/POJ-1679
题意 判断最小生成树是否唯一
思路枚举最小生成树的n条边，每次减去一条边，看最小生成树是否存在

弱思维

Cartesian MST

题面：求两个树的笛卡尔积产生的树的最小生成树。

如图：

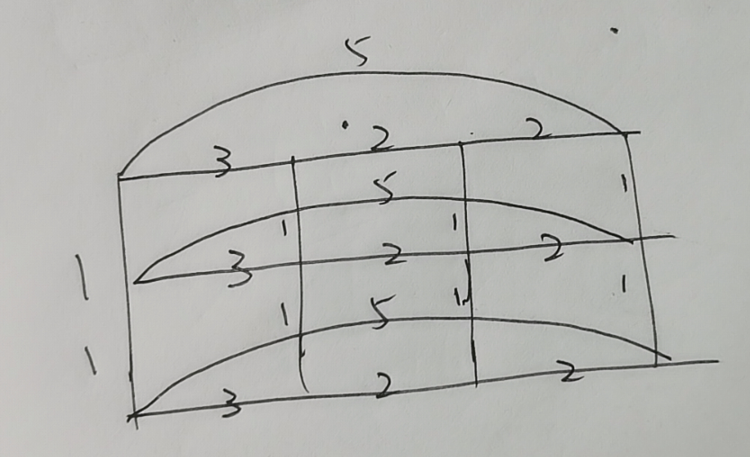
思路：这个画个图，模拟一下应该不难想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
/*
* @Author: Marhoosh
* @Date:   2021-07-22 10:27:41
* @Last Modified by:   Marhoosh
* @Last Modified time: 2021-10-13 14:25:30
*/
#include<bits/stdc++.h>
#pragma comment(linker, "/STACK:102400000,102400000")
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
#define INF 0x7fffffff
typedef long long ll;
typedef pair<ll,ll> P;
const ll maxn=2e5+11;
struct Edge{
    ll fr,to,w,type;
    bool operator < (const Edge& b) const {
        return w<b.w;
    }
}e[maxn];
ll f1[maxn],f2[maxn];
ll n1,m1,n2,m2;
ll found1(ll x){
    return f1[x]==x?x:f1[x]=found1(f1[x]);
}
ll found2(ll x){
    return f2[x]==x?x:f2[x]=found2(f2[x]);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n1>>m1>>n2>>m2;
    for(ll i=0;i<n1;i++)  f1[i]=i;
    for(ll i=0;i<n2;i++)  f2[i]=i;
    ll tmp=0;
    for(ll i=1;i<=m1;i++){
        ll u,v,w;cin>>u>>v>>w;
        e[tmp++]={u,v,w,1};
    }
    for(ll i=1;i<=m2;i++){
        ll u,v,w;cin>>u>>v>>w;
        e[tmp++]={u,v,w,2};
    }
    sort(e,e+tmp);
    ll cnt=0,cnt1=0,cnt2=0,p=0,ans=0;
    while(cnt<=n1+n2-2 && p<tmp){
        ll ty=e[p].type;
        if(ty==1){
            if(cnt1>=n1-1){
                p++;continue;
            }
            ll u=e[p].fr,v=e[p].to;
            ll fu=found1(u),fv=found1(v);
            if(fu==fv){
                p++;continue;
            }  
            f1[fu]=fv;
            ans=ans+(n2-cnt2)*e[p].w;
            cnt1++;cnt++;p++;
        }
        else{
            if(cnt2>=n2-1){
                p++;continue;
            }
            ll u=e[p].fr,v=e[p].to;
            ll fu=found2(u),fv=found2(v);
            if(fu==fv){
                p++;continue;
            } 
            f2[fu]=fv;
            ans=ans+(n1-cnt1)*e[p].w;
            cnt2++;cnt++;p++;
        }
    }
    cout<<ans<<endl;
    return 0;
}

prim

  • 思路 感觉本质上就是kruskal，与kruskal思路没啥区别，要说区别就是kruskal过程上是加边，这个是过程上加点吧，但其实都是每次选择权值最小的边，都是贪心。
  • 具体方法 弄两个点集，一个u，一个v，每次选择一个端点在u，一个端点在v产生的边中，权值最小的边，并把在v中的点，加入u中。
  • 链式前向星模板 时间O(n*n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
//链式前向星-----------------------------------------------------------------------------
/*** 
 * @Practice Win
 * 畅通工程 HDU - 1863 
 * prim
 * 最小生成树 板子题
 */
#include<bits/stdc++.h>
#pragma comment(linker, "/STACK:102400000,102400000")//解决递归函数多次调用栈溢出问题
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
typedef long long ll;
#define INF 0x7fffffff//10^9级别，不到2^32
const ll maxn=1e2+11;//最大顶点数
struct Edge{
	ll fr,to,w,next;
}edge[maxn*maxn];
ll head[maxn],vis[maxn],dis[maxn];
ll n,m,tmp;
ll prim(){//若存在最小生成树，返回其值并输出，否则返回一个未知值，并输出"?"
	ll minn=INF,pos,ans=0;
	for(ll i=head[1];~i;i=edge[i].next){//从顶点编号1开始初始化
		ll v=edge[i].to;
		dis[v]=min(dis[v],edge[i].w);//考虑有重边情况！！！
	}
	vis[1]=1;
	for(ll i=2;i<=n;i++){ 
		ll minn=INF;
		pos=-1;
		for(ll j=1;j<=n;j++)  if(!vis[j] && dis[j]<minn)  minn=dis[j],pos=j;
		if(pos==-1)  break;
		vis[pos]=1;
		ans+=minn;
		for(ll i=head[pos];~i;i=edge[i].next){
			ll v=edge[i].to;
			if(edge[i].w<dis[v])  dis[v]=edge[i].w;
		}
	}
	if(pos==-1)  cout<<"?"<<endl;
	else  cout<<ans<<endl;
	return ans;
}
void add(ll u,ll v,ll w){
	edge[tmp].fr=u; edge[tmp].to=v; edge[tmp].w=w;
	edge[tmp].next=head[u];
	head[u]=tmp++;
}	
void init(){
	memset(vis,0,sizeof(vis));
	memset(head,-1,sizeof(head));
	memset(dis,0x3f3f3f3f,sizeof(dis));
	tmp=1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
	while(cin>>m>>n && m){
		init();
		for(ll i=1;i<=m;i++){
			ll u,v,w;
			cin>>u>>v>>w;
			add(u,v,w);
			add(v,u,w);
		}
		prim();
	}
    return 0;
}
  • 邻接矩阵模板 时间O(n*n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//邻接矩阵-----------------------------------------------------------------------------
/*** 
 * @Practice Win
 * 畅通工程 HDU - 1863 
 * prim
 * 最小生成树 板子题
 */
#include<bits/stdc++.h>
#pragma comment(linker, "/STACK:102400000,102400000")//解决递归函数多次调用栈溢出问题
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
typedef long long ll;
#define INF 0x7fffffff//10^9级别，不到2^32
const ll maxn=1e2+11;//最大顶点数
ll vis[maxn],dis[maxn],gra[maxn][maxn];
ll n,m;
ll prim(){//若存在最小生成树，返回其值并输出，否则返回一个未知值，并输出"?"
	ll minn=INF,pos,ans=0;
	for(ll i=1;i<=n;i++)  dis[i]=gra[1][i];
	vis[1]=1;
	for(ll i=2;i<=n;i++){ 
		ll minn=INF;
		pos=-1;
		for(ll j=1;j<=n;j++)  if(!vis[j] && dis[j]<minn)  minn=dis[j],pos=j;
		if(pos==-1)  break;
		vis[pos]=1;
		ans+=minn;
		for(ll j=1;j<=n;j++)  if(!vis[j] && gra[pos][j]<dis[j])  dis[j]=gra[pos][j];
	}
	if(pos==-1)  cout<<"?"<<endl;
	else  cout<<ans<<endl;
	return ans;
}
	
void init(){
	memset(vis,0,sizeof(vis));
	memset(dis,0x3f3f3f3f,sizeof(dis));
	memset(gra,0x3f3f3f3f,sizeof(gra));
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
	while(cin>>m>>n && m){
		init();
		for(ll i=1;i<=m;i++){
			ll u,v,w;
			cin>>u>>v>>w;
			if(w<gra[u][v])  gra[u][v]=gra[v][u]=w;
		}
		prim();
	}
    return 0;
}

灵活运用（已建立某些边）

继续畅通工程
题意 在有些边已经建立好了的情况下，求最小生成树。
思路 对于已经建立的边，将其权值变为0即可。

灵活运用（已知每个点的代价）

Shichikuji and Power Grid
常见最小生成树是知道每条边的代价，这题增加了一个就是还知道每个点的代价。
题面
有n个城市,坐标为(xi,yi),还有两个系数ci,ki.在每个城市建立发电站需要费用ci.如果不建立发电站，要让城市通电，就需要与有发电站的城市连通。i与j之间连一条无向的边的费用是(ki+kj)*两个城市之间的曼哈顿距离.求让每个城市都通电的最小费用,并输出任意一个方案。

分析
我刚开始想的就是，这不就是prim，然后将dis[i]初始化为每个点的代价嘛，然后发现这是个常见套路，也可以把选每个点的代价转成虚拟原点到这个点的边,不过这样子更好理解。这个套路很常见，但在最小生成树题里还是第一次见到。

城市之间两两连边，边权按题目里提到的计算。然后建立一个虚拟源点，向每个城市i连边，边权为ci.对整个图跑一个最小生成树即可.

  • 总结

  • 两者区别这个方法的好处就是，因为分成了两个点集合，所以保证了选择的权值最小的边肯定不会产生环，因为这个边的端点分别在两个互斥的集合嘛，不像kruskal选择的边可能都在集合u。

  • 稀疏图与稠密图数据结构中对于稀疏图的定义为：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图（sparse graph），反之边的条数|E|接近|V|²，称为稠密图（dense graph）。此定义来自百度百科，实际上是一种朴素的理解，简单来说边越多，图就越稠密

  • 两者复杂度
    Kruskal:
    在这里插入图片描述
    Prim:
    在这里插入图片描述