二分图的构造

发表于2021-10-30更新于2021-10-30

Bigraph Extension HDU - 7135

有一个2*n（n为偶数，n < 1e3)个点的二分图，已经连好了m条边，这m条边保证任意两条边不含公共点。
求最少添加多少条边，使得这个图任意两点连通，且最长简单路径所含边数 > n。输出最小字典序的方案。



``
`





`



``

``

``
思路，不难想到是要建一个2*n的环。那么此题关键点是要构造字典序最小的方案，那么我们每次找字典序最小的点来建边即可。用并查集维护，保证连的点不成环。
那么对于最后一条边，也就是两个度数为1的点连边使图成环即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/*
* @Author: Marhoosh
* @Date:   2021-10-11 11:00:11
* @Last Modified by:   Marhoosh
* @Last Modified time: 2021-10-30 15:52:27
*/
#include<bits/stdc++.h>
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
#define INF 0x7fffffff
typedef long long ll;
typedef pair<ll,ll> P;
const ll maxn=2e3+11;
vector<P> ans;
ll fa[maxn],d[maxn];
ll n,m;
ll found(ll x){return fa[x]==x?x:fa[x]=found(fa[x]);}
void solve1(){
    ll e=0;
    for(ll i=1;i<=n;i++){
        while(d[i]<2){
            for(ll j=n+1;j<=2*n;j++){
                if(d[j]<2){
                    ll fi=found(i),fj=found(j);
                    if(fi==fj)  continue;
                    d[i]++,d[j]++;
                    ans.push_back({i,j});
                    //cout<<i<<" "<<j<<endl;
                    fa[fi]=fj;
                    e++;
                    if(e>=2*n-m-1)  return ;
                    break;
                }
            }
        }
    }
}
void solve2(){
    ll u,v;
    for(ll i=1;i<=2*n;i++){
        if(d[i]==1){u=i;break;}
    }
    for(ll i=1;i<=2*n;i++){
        if(d[i]==1 && i!=u){v=i;break;}
    }
    ans.push_back({u,v});
    cout<<ans.size()<<endl;
    for(auto i=ans.begin();i!=ans.end();i++){
        cout<<(*i).first<<" "<<(*i).second-n<<endl;
    }
    return ;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    ll ca;cin>>ca;
    while(ca--){
        cin>>n>>m;
        for(ll i=1;i<=2*n;i++)  fa[i]=i;
        ans.clear();memset(d,0,sizeof(d));
        for(ll i=1;i<=m;i++){
            ll u,v;cin>>u>>v;
            v=v+n;
            d[u]++,d[v]++;
            fa[u]=v;
        }
        solve1();
        solve2();
    }
    return 0;
}

数学+树状数组

发表于2021-10-25更新于2021-10-25

Master of Sequence





`


`









这是个向下取整求和问题。
不难想到，应该二分t，但复杂度是O(n*logn)的，有m次询问，总共是O(m * n * logn)。即使给了10s，但是由于hdu的评测机实在不行，
6e9居然10s也跑不完。。，所以得优化一下。这道题需要注意到ai范围只有1000，所以我们可以把相同的ai值一起来求和，优化复杂度。
对于相同的ai值求和，即向下取整求和，关键是处理这个模数问题。所以我们把式子的模数处理出来，[ t-bi/ai ]化为[ k1 * ai+t%ai - ( k2 * ai+bi%ai )/ai ]。
即k1-k2+[ (t%ai-bi%ai)/ai ]，记k1=t/ai,k2=bi/ai,c1=t%ai,c2=bi%ai,[ ( c1-c2 )/ai ]当且仅当c1 < c2时为-1，否则为0.故我们只需要每次统计 分母为ai时大于c1的c2个数即可.于是我们用f[ x ][ y ]表示当ai为x时，1 <=bi%ai+1<=y的bi个数。用树状数组来维护这个区间和即可。ai==x的个数就为f[ x ][ 1000 ]。
于是答案就为:

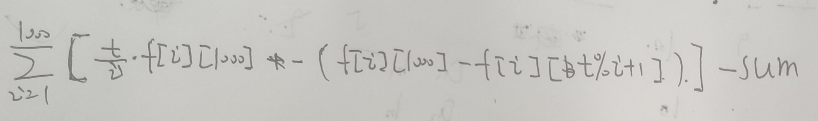
sum为ai==i从1~1000，bi/ai的和。

踩坑：因为树状数组左端点不能为0，不然update会死循环，但是bi%ai可以为0，所以我们统一将bi%ai+1.
踩坑：一开始没用num[ i ]统计ai为i时，ai的个数，用的时getsum(1000)超时了，改了之后是时间限制的一半，怪不得会超时。常数大了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
//两个错误,bi/ai弄错了
//bi%ai在树状数组中不能存0
//getsum()多写了几个超时了... 醉了  
/*
* @Author: Marhoosh
* @Date:   2021-10-11 11:00:11
* @Last Modified by:   Marhoosh
* @Last Modified time: 2021-10-25 20:49:09
*/
#include<bits/stdc++.h>
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
#define INF 0x7fffffff
typedef long long ll;
typedef pair<ll,ll> P;
const ll maxn=1e5+11;

ll f[1111][1111],a[maxn],b[maxn],num[1111];
ll n,m,sum;

ll lowbit(ll x){return x & -x;}
void update(ll i,ll x,ll val){for(;x<=1000;f[i][x]+=val,x+=lowbit(x));}
//update,x为0时死循环

ll getsum(ll i,ll x){ll sum=0;for(;x>=1;sum+=f[i][x],x-=lowbit(x));return sum;}

ll check(ll mid,ll k){
    ll ans=0;
    for(ll i=1;i<=1000;i++){
        ans=ans+mid/i*num[i];
        ans=ans-num[i]+getsum(i,mid%i+1);
    }
    ans-=sum;
    if(ans>=k)  return 1;
    else  return 0;
}

void solve(ll k){
    ll l=0,r=1e9+11;
    while(l<r){
        ll mid=(l+r)/2;
        if(check(mid,k))  r=mid;
        else  l=mid+1;
    }
    printf("%lld\n",l);
}

int main(){
    ll ca;scanf("%lld",&ca);
    while(ca--){
        memset(f,0,sizeof(f));memset(num,0,sizeof(num));
        sum=0;
        scanf("%lld%lld",&n,&m);
        for(ll i=1;i<=n;i++)  scanf("%lld",&a[i]);
        for(ll i=1;i<=n;i++){
            scanf("%lld",&b[i]);
            sum+=b[i]/a[i];
            update(a[i],b[i]%a[i]+1,1);
            num[a[i]]++;
        }
        for(ll i=1;i<=m;i++){
            ll type;scanf("%lld",&type);
            if(type==1){
                ll x,y;scanf("%lld%lld",&x,&y);
                sum-=b[x]/a[x];
                sum+=b[x]/y;
                update(a[x],b[x]%a[x]+1,-1);
                num[a[x]]--;
                update(y,b[x]%y+1,1);
                num[y]++;
                a[x]=y;
            }
            else if(type==2){
                ll x,y;scanf("%lld%lld",&x,&y);
                sum-=b[x]/a[x];
                sum+=y/a[x];
                update(a[x],b[x]%a[x]+1,-1);
                num[a[x]]--;
                update(a[x],y%a[x]+1,1);
                num[a[x]]++;
                b[x]=y;
            }
            else{
                ll k;scanf("%lld",&k);
                solve(k);
            }
        }
    }
    return 0;
}

贪心思维

发表于2021-10-25更新于2021-10-25

Neko’s loop HDU - 6444

题意：有n个城市, 在每个城市中你可以选择花费a[ i ]的价格买一个能量块, 也可以选择以a[ i ]的价格卖出一个能量块(前提是你要有能量块可以卖). 你会从1号城市依次走到n号城市, 每次可以选择买或者卖或者什么也不做. 在初始你有无限多的钱的前提下, 问你能获得的最大利润, 以及在最大利润的前提下最小的买卖次数.
————————————————
版权声明：本文为CSDN博主「逍遥Fau」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_45799835/article/details/108682519

·
·

·
·
·
·
·
·
·

·
·
·
·
·

·
·

·
·
·
·
·

·
·
·
·
·

·
解题思路:
首先如果一件物品买了后再卖了能赚钱, 则我们一定会采取这种方案, 因为题目要求最大利润优先, 最小的买卖次数则是不做无意义的买卖, 如花费x元购买能量块后又以x元卖出.

贪心思路:
因为我们难以决定在第i个城市我们采取怎么样的操作是最优的, 所以不妨对于每一个城市, 我们都认为我们可以从该城市买入能量块, 并且在j城市(j>i)卖出(但是在卖出之前, 我们认为我们在i城市什么也没做). 而j城市的能量块价格是一定为a[j]的, 所以此时我们如果要卖出能量块, 一定要以最小的价格在i城市买入能量块. 对于买入能量块的城市i, 我们可以采用小顶堆来维护, 而城市j的确定则是难点.

假设我们现在存在一个小顶堆, 里面存放的元素代表可以用x的价格买入能量块(即所有的i城市), 当我们到达j城市, 此时如果满足a[j] > heap.top(), 我们此时选择卖出一定可以赚到钱, 且为一种优质策略.
此时我们的利润变化为: res = res + a[j] - x. (记为*式)

但是我们无法保证后续不会存在城市k (k>j), 满足a[k] > a[j], 则我们发现不如在k城市卖出刚才的能量块, 所以我们此时就要有一种反悔策略, 即: 刚才的能量块不选择在j城市卖出(即我们又可以以a[j]的价格买入能量块, 应当把a[j]入堆), 而在k城市卖出该能量块. 本身我们花费了x元买入, 卖出得到了a[j]元, 变成了x元买入, a[k]元卖出. 则利润变化为: res = res - a[j] + a[k]. 做一个变形, 类比于*式, 我们得到 res = res + a[k] - a[j].
从操作次数的角度看, 我们在j城市买入能量块, 在k城市卖出, 结合之前i城市的操作, 相当于我们在j城市卖了一次, 又买了一次. 所以在j城市的操作并不是合法操作, 不应计算在结果中.

而从利润的角度看, 我们获得的利润可以看作买了i, 在j卖出, 又在j买入, 在k卖出. 我们发现这两种情况的利润遵循相同的公式.
————————————————
版权声明：本文为CSDN博主「逍遥Fau」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_45799835/article/details/108682519

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
* @Author: Marhoosh
* @Date:   2021-07-22 10:27:37
* @Last Modified by:   Marhoosh
* @Last Modified time: 2021-10-25 13:07:14
*/
#include<bits/stdc++.h>
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
#define INF 0x7fffffff
typedef long long ll;
typedef pair<ll,ll> P;
const ll maxn=2e5+11;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    ll ca;cin>>ca;
    while(ca--){
        ll n;cin>>n;
        priority_queue<ll,vector<ll>,greater<ll>> q;
        map<ll,ll> mp;
        ll ans=0,cnt=0;
        for(ll i=1;i<=n;i++){
            ll x;cin>>x;
            if(!q.empty() && q.top()<x){
                ll sell=q.top();q.pop();
                ans+=x-sell;
                if(mp.count(sell)){
                    if(--mp[sell]==0)  mp.erase(sell);
                    q.push(sell);
                }
                else  cnt++;
                mp[x]++;
            }
            q.push(x);
        }
        cout<<ans<<" "<<cnt*2<<endl;
    }
    return 0;
}

树状数组+DP

发表于2021-10-24更新于2021-10-24

YJJ’s Salesman

题意：A从(0,0)走到(1e9,1e9)，规定只能向下走，向右走，向右下走。在二维平面上有n < 1e5个村庄，
每个村庄有一个奖励值，规定只有从左上方向来到达村庄方可获得奖励值，问最多可以获得多少奖励值。












很显然有DP[ i ][ j ]=DP[i-1][j]+DP[i][j-1]+DP[i-1][j-1];
但是这需要DP[1e5][1e5]才可以操作，显然不行。
于是我们考虑只遍历每个点。

踩坑：DP更新的时候，只能从右往左更新，因为它是要求从左上方下来才可以，这样子就不包含从左来的点。如果从左往右更新，那么就包含了从左来的点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/*
* @Author: Marhoosh
* @Date:   2021-07-22 10:27:29
* @Last Modified by:   Marhoosh
* @Last Modified time: 2021-10-24 21:17:24
*/
//优化遍历问题
#include<bits/stdc++.h>
using namespace std;
#define Debug(x) cout<<#x<<':'<<x<<endl
#define INF 0x7fffffff
typedef long long ll;
typedef pair<ll,ll> P;
const ll maxn=1e5+11;
struct Point{
    ll x,y,w;
    bool operator < (const Point &b) const {
        if(y==b.y)  return x>b.x;//需要从右向左更新
        return y<b.y;
    }
}p[maxn];
ll f[maxn],x[maxn];
ll n;

ll lowbit(ll x){return x & -x;}

void update(ll x,ll val){
    for(;x<=n;f[x]=max(val,f[x]),x+=lowbit(x));
}

ll query(ll x){
    ll ans=0;
    for(;x>=1;ans=max(ans,f[x]),x-=lowbit(x));
    return ans;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    ll ca;cin>>ca;
    while(ca--){
        memset(f,0,sizeof(f));
        cin>>n;
        for(ll i=1;i<=n;i++){
            ll y,w;cin>>x[i]>>y>>w;
            p[i]={x[i],y,w};
        }
        sort(p+1,p+n+1);
        sort(x+1,x+n+1);
        ll l=unique(x+1,x+n+1)-(x+1);
        for(ll i=1;i<=n;i++){
            p[i].x=lower_bound(x+1,x+l+1,p[i].x)-x;
        }    
        for(ll i=1;i<=n;i++){
            ll uu=query(p[i].x-1)+p[i].w;
            update(p[i].x,uu);
        }
        cout<<query(l)<<endl;    
    }
    return 0;
}

小学数学

发表于2021-10-24更新于2021-10-24

Find Integer

``


`
``








`
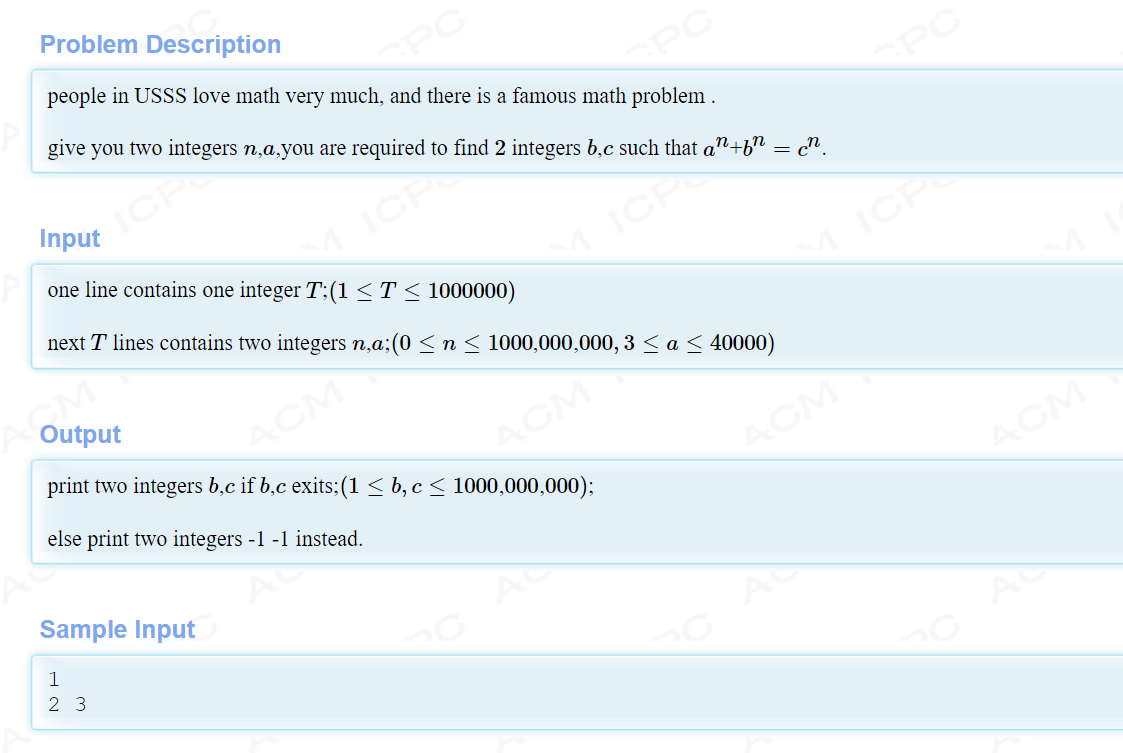
用费马大定理可证n > 2的时候无解。
打表也可以发现此规律
n==2的时候，a * a=(c-b) * (c+b);
让c-b==1 和c-b==2，
分a奇偶讨论即可。